Drzewa BST
BST = Binary Search Tree = drzewo poszukiwań binarnych
Drzewo BST to drzewo binarne (niekoniecznie pełne), posiadające "własność
drzewa BST".
Każdy wierzchołek "x" drzewa BST posiada (przynajmniej) następujące
pola:
x.klucz <-- liczba całkowita
x.ojciec, x.lewy, x.prawy <-- wskazania na inne wierzchołki drzewa
Własność drzewa BST:
niech "x" będzie dowolnym wierzchołkiem drzewa;
wszystkie wierzchołki lewego poddrzewa wierz "x" mają klucze
< x.klucz
wszystkie wierzchołki prawego poddrzewa wierz "x" mają klucze
> x.klucz
|
Przykład drzewa BST:
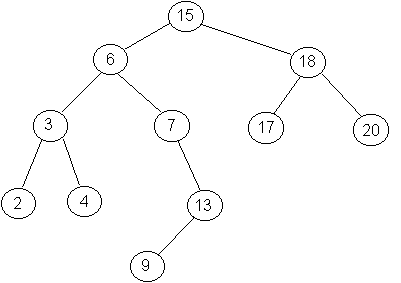
Założenie:
Dla uproszczenia zakładamy że wszystkie klucze w drzewie BST są różne
!
Do czego służą drzewa BST ?
-
do implementacji słowników...
w każdym wierzchołku przechowujemy oprócz klucza także wartość;
para (klucz,wartość) jest elementem słownika; do slownika można wrzucić
wiele takich elementów; potem podajemy klucz a słownik zwraca odpowiadającą
mu wartość (chodzi o szybkość wykonywania tych operacji)
-
do implementacji kolejek priorytetowych...
do takiej kolejki wrzuca się elementy zaopatrzone w priorytet
(=klucz); potem wyciągamy z kolejki element z największym priorytetem i
usuwamy go z kolejki (znów drzewa BST maja zapewnić dużą szybkość wykonywania
tych operacji)
Jest wiele innych możliwych zastosowań. Okazuje się że podstawowe operacje
na drzewach BST wymagają czasu równego wysokości drzewa. Problem polega
na tym że nie zawsze można zagwarantować małą wysokość drzewa - zależy
to od sposobu tworzenia drzewa - od kolejności w jakiej wstawiamy wierzchołki
drzewa.
Uwagi implementacyjne:
Wierzchołki drzewa BST muszą być tworzone "dynamicznie", należy używać
"wskazań".
Wierzchołek drzewa BST reprezentujemy przy pomocy struktury/rekordu
BST_Wierz :
// język C ----------------------------
//
struct BST_Wierz {
int klucz;
// można dodać także jakąś "wartość"
BST_Wierz *ojciec; // wskazanie na "ojca" wierzchołka
BST_Wierz *lewy, *prawy; // wskazania na lewego i prawego "potomka"
};
main()
{
BST_Wierz *w=new BST_Wierz;
w->klucz=1234;
w->ojciec=NULL; w->lewy=NULL; w->prawy=NULL;
delete w;
}
{
język Pascal ------------------------
}
type
BST_WierzWsk=^BST_Wierz;
BST_Wierz=record
klucz:integer;
{ można dodać także jakąś "wartość" }
ojciec:BST_WierzWsk;
lewy,prawy:BST_WierzWsk;
end;
var
w:BST_WierzWsk;
begin
new(w);
w^.klucz:=1234;
w^.ojciec:=nil; w^.lewy:=nil; w^.prawy:=nil;
dispose(w);
end.
Oto podstawowe operacje na drzewie BST:
void BST_WstawWierz(BST_Wierz *&korzen, int klucz);
void BST_WstawWierz(BST_Wierz *&korzen, BST_Wierz *wierz);
// "korzen" to wskazanie na korzen drzewa BST
// (musi być możliwość modyfikowania go - stąd "&")
void BST_PokazInorder(BST_Wierz *korzen);
// pokazuje klucze w kolejnosci od najmniejszego do największego
// inne możliwości to "preorder" i "postorder"
BST_Wierz *BST_Znajdz(BST_Wierz *korzen, int klucz);
// jeśli element o podanym kluczu nie istnieje to zwracamy NULL
BST_Wierz *BST_Maksimum(BST_Wierz *korzen);
BST_Wierz *BST_Minimum(BST_Wierz *korzen);
// zwraca wsk na wierzchołek z maksymalnym/mininalnym kluczem
BST_Wierz *BST_Nastepnik(BST_Wierz *wierz);
BST_Wierz *BST_Poprzednik(BST_Wierz *wierz);
// następnik/poprzednik "względem kluczy"
void BST_UsunWierz(BST_Wierz *&korzen, BST_Wierz *wierz);
Zadanie 20
Zaimplementuj poniższe procedury, posiłkując się wskazówkami.
Odpowiedz także na pytania (dlaczego ?); można się posiłkować
powyższym rysunkiem.
Zademonstruj działanie procedur na małym przykładzie.
-
void BST_WstawWierz(BST_Wierz *&korzen, int klucz);
void BST_WstawWierz(BST_Wierz *&korzen, BST_Wierz
*wierz);
-
oczywiście nowy wierzchołek należy wstawiać tak aby
nie popsuć własności drzewa BST;
-
nowy wierzchołek wstawiamy zawsze jako liść drzewa,
należy tylko wyszukać odpowiednie miejsce: sprawdzamy czy "klucz" jest
>= od "korzen->klucz" jeśli tak to wierzchołek zostanie wstawiony w prawym
poddrzewie, w przeciwnym wypadku w lewym poddrzewie itd ...
-
.
-
void BST_PokazInorder(BST_Wierz *korzen);
-
przechodzić drzewo metodą "inorder", tj najpierw rekurencyjne wywołanie
dla lewego poddrzewa, potem wypisanie klucza bieżącego wierchołka, potem
rekurencyjne wywołanie dla prawego poddrzewa
-
void BST_PokazPreorder2(BST_Wierz *korzen);
-
przechodzić drzewo metodą "preorder", tj najpierw wypisanie klucza, potem
rekurencyjne wywołanie dla lewego poddrzewa, potem rekurencyjne wywołanie
dla prawego poddrzewa; dodatkowo dla każdego klucza podajemy klucz jego
ojca; np "5() 2(5) 8(5) 7(8) 9(8)"
-
.
-
BST_Wierz *BST_Znajdz(BST_Wierz *korzen, int klucz);
-
oczywista rekurencja; jeśli bieżący wierzchołek nie ma poszukiwanego klucza
to wiemy w którym poddrzewie (lewym czy prawym) może się poszukiwany klucz
znajdować na podstawie "własności drzewa BST"
-
.
-
BST_Wierz *BST_Maksimum(BST_Wierz *korzen);
-
wystarczy "iść" po prawej gałęzi drzewa BST, w kierunku od korzenia do
liści, tak długo jak to możliwe
-
.
-
BST_Wierz *BST_Nastepnik(BST_Wierz *wierz);
-
1) jeśli "wierz" posiada prawe poddrzewo, to wtedy zwracamy minimalny element
w prawym poddrzewie (dlaczego ?)
-
2) w przeciwnym wypadku szukamy wierzchołka takiego, że największym kluczem
jego lewego poddrzewa jest "wierz->klucz"; innymi słowy idziemy od wierzchołka
"wierz" w górę drzewa tak długo aż napotkamy wierzchołek, który jest lewym
synem swojego ojca; klucz ojca jest właśnie poszukiwanym następnikiem (na
powyższym rysunku następnikiem 13 jest 15)
-
.
