Strona Michała Hańćkowiaka, ASD220

Zadanie 21

Przypuśćmy, że mamy losową permutację kluczy ze zbioru {1, ..., N}.
Tworzymy drzewo BST uruchamiając proc BST_WstawWierz() dla kolejnych kluczy z tej permutacji.
W książce Cormena (str 299) udowodniono, że oczekiwana wysokość tak otrzymanego drzewa wynosi:

O(log N) Sprawdź to eksperymentalnie.

Będzie potrzebna procedura tworząca N-elementową losową permutację

void GenerowaniePermutacji() w tablicy "int Permutacja[10240]" (wszystkie równo prawdopodobne),
oraz procedura obliczająca wysokość drzewa

int BST_Wysokosc(BST_Wierz *korzen);

a także procedura do usuwania całego drzewa z pamięci

void BST_UsunDrzewo(BST_Wierz *&korzen);

.
Aby oszacować wartość oczekiwaną należy wykonać 50 prób i "uśrednić".
Jak sprawdzić czy coś jest rzędu O(log N) ? Wykorzystaj:

log (2N) = 1 + log N Pamiętaj o stałej ukrytej w O() !

Oprócz procedury BST_Wysokosc() dodaj mechanizm obliczania wysokości podczas wykonywania BST_WstawWierz() na permutacji. Dodaj kontrolę czy oba sposoby obliczania wysokości są ze sobą zgodne. Pamiętaj że wysokość drzewa pustego i jedno-wierzchołkowego wynosi 0.

Program musi wydrukować coś podobnego do:

    coreleft()=516704
    N=   10; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N=   20; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N=   40; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N=   80; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N=  160; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N=  320; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N=  640; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N= 1280; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N= 2560; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N= 5120; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    N=10240; ilosc= 50; srednia wysokosc= ???.?? ; min= ??; max= ??
    coreleft()=516704

Uwaga (jeśli używamy języka C):
podczas programowania BST_Wysokosc() należy mieć na uwadze że makro max(a,b) może być zdefiniowane następująco

#define max(a,b) (((a)>=(b))?(a):(b)) tak więc wywolanie rekurencyjne

max(BST_Wysokosc(x->lewy),BST_Wysokosc(x->prawy)) pociąga za sobą dwukrotne wywolanie procedur (ma to bardzo negatywne skutki !)

Zadanie 22

Zaimplementuj następującą procedure usuwania wierzchołka z drzewa BST:

void BST_UsunWierz(BST_Wierz *&korzen, BST_Wierz *wierz); Uwaga: ta procedura jest dość skomplikowana !
należy rozważyć trzy przypadki:
1) "wierz" jest liściem drzewa - wtedy zwyczajnie go usuwamy
2) "wierz" ma tylko jednego potomka - wtedy dodajemy plączenie między "wierz->ojciec" i "wierz->lewy" (lub "wierz->prawy"), a sam "wierz" usuwamy
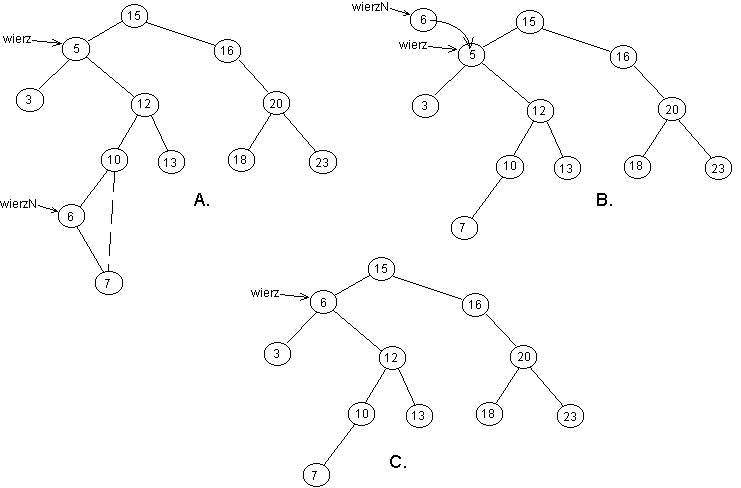
3) "wierz" ma dwóch potomków - wtedy znajdujemy następnik "wierz"; oznaczmy go przez "wierzN"; o "wierzN" wiemy że nie ma lewego potomka (dlaczego ?); dodajemy polączenie między "wierzN->ojciec" i "wierzN->prawy", następnie przepisujemy "wierzN->klucz" do "wierz->klucz" i usuwamy "wierzN".

Należy wypróbować działanie tej procedury na małym drzewie (wyświetlając drzewo procedurą BST_PokazPreorder2 po usunięciu każdego wierzchołka).

Trzeci punkt tej procedury jest przedstawiony na poniższym rysunku:

Zadanie 23

Zaimplementuj "kolejkę priorytetową" na której można wykonywac następujące operacje:

BST_Wierz *PRI_WyciagnijMin(BST_Wierz *&korzen)
BST_Wierz *PRI_WyciagnijMax(BST_Wierz *&korzen)

procedury te zwracają wskaznik do wierzchołka z min/max kluczem oraz usuwają ten wierzchołek z drzewa BST (ale nie usuwają go "fizycznie" !) void PRI_ZmienKlucz(BST_Wierz *&korzen, BST_Wierz *wierz, int nowyKlucz)

procedura zmienia klucz wierzchołka "wierz" zachowując własność drzewa BST; wierzchołek ten NIE MOŻE zmienić miejsca w pamięci podczas tej operacji Zauważmy że procedury te mogą zmienić korzeń drzewa, dlatego jest on przekazywany "przez zmienną".
Wypróbuj działanie kolejki na niewielkiej liczbie elementów.

Zadanie 24

(implementacja grafów przy pomocy list sąsiedztw)

Zaimplementuj procedury i strukury danych do reprezentowanie grafów przy pomocy list sąsiedztw czyli w następujący sposób:

Na powyższym rysunku każdemu wierzchołkowi grafu jest przyporządkowana lista jego sąsiadów, a dokładniej lista indeksów jego sąsiadów (wagi nie będą chwilowo używane).

Grafem skierowanym nazywamy graf na którego krawędziach narysowano strzałki.

W przypadku grafów skierowanych dla każdego wierzchołka pamiętamy liste jego sąsiadów wychodzących.
W przypadku grafów nieskierowanych dla każdego wierzchołka pamiętamy liste wszystkich jego sąsiadów (co oznacza ze każda krawędź jest pamiętana 2 razy !).

Zaimplementuj procedury:

struct Graf {
  int N; // liczba wierzchołków
  // oraz cala reszta
};

struct GrafSkierowany {
  int N; // liczba wierzchołków
  // oraz cala reszta
};

void DodajKraw(Graf &g, int u, int v);
void DodajKraw(GrafSkierowany &g, int u, int v);

void UsunKraw(Graf &g, int u, int v);
void UsunKraw(GrafSkierowany &g, int u, int v);

void PokazGraf(Graf &g);
void PokazGraf(GrafSkierowany &g);

Kwestię inicjowania struktur Graf i GrafSkierowany, oraz to czy tablica wierzchołków jest przydzielana dynamicznie czy nie pozostawiam wykonawcy zadania do rozstrzygnięcia.
Sprawdź czy wszytko działa na małym przykładzie.

Zadanie 24a

Zaprogramuj procedurę konstruującą "transpozycje grafu skierowanego", czyli odwracająca strzałki na wszystkich krawędziach.

void TranspozycjaGrafu(GrafSkierowany &g1, GrafSkierowany &g2);

// g1 - wejscie, g2 - wyjscie Wypróbuj działanie procedury na małym grafie (używając PokazGraf(GrafSkierowany &g)).
Dokonaj analizy czasu działania tej procedury (|V|=liczba wierzchołków grafu, |E|=liczba krawędzi grafu).

Zadanie 24b

Zaprogramuj procedurę konstruującą "kwadrat grafu skierowanego".
Niech G2 oznacza kwadrat grafu G. Graf G2 ma krawedz (a,b) jesli w G isnieje skierowana scieżka a,x,b dla pewnego wierzchołka x.

void KwadratGrafu(GrafSkierowany &g1, GrafSkierowany &g2);