Strona Michała Hańćkowiaka, ASD220

Drzewa czerwono-czarne (drzewa RB).

Drzewa RB to drzewa BST z pewnymi dodatkowymi ulepszeniami, które powodują że podczas wstawiania i usuwania wierzchołków drzewo zachowuje wysokość rzędu O(log n), gdzie n jest liczbą wierzchołków. Dzięki temu wszystkie operacje na drzewie (wyszukiwanie elementu o zadanym kluczu itp) są wykonywane w czasie O(log n).

Drzewo RB to drzewo BST, w którym każdy wierzchołek posiada dodatkowe pole "kolor" i które posiada tzw własności czerwono-czarne:

każdy wierzchołk jest czerwony lub czarny
każdy liść jest czarny
jeśli wierzchołek jest czerwony to ma dwóch synów i obaj są czarni
każda prosta ścieżka z ustalonego wierzchoła do liścia ma tyle samo czarnych wierzchołków

UWAGA 1:
Liście drzewa RB nie istnieją "fizycznie"; jeśli pewien wierzchołek "x" ma
x->lewy == x->prawy == NULL
to traktujemy go jako wierzchołek wewnętrzny drzewa, z dwoma wystającymi liśćmi
(liście są reprezentowane przez wartości NULL; liście nie mają kluczy; przyjmujemy że liście mają kolor czarny)

UWAGA 2:
Wszystkie operacje z drzew BST (za wyjątkiem wstawiania i usuwania wierzchołków) można przenieść na drzewa RB. Operacje BST_WstawWierz() i BST_UsunWierz() zniszczyłyby własności czerwono-czarne !.

UWAGA 3:
Z własności czerwono-czarnych 3 i 4 wynika że ścieżki łączące korzeń i liście mają długości różniące się co najwyżej o czynnik 2. Dlatego właśnie drzewo RB jest w przybliżeniu zrównoważone i ma wysokość O(log n).

DEF: liczbę czarnych wierzchołkow na dowolnej ścieżce od wierz "x" do liścia (wykluczając "x") nazywamy czarną wysokością wierzchołka "x".

Wierzchołek drzewa RB reprezentujemy przy pomocy struktury:

struct RB_Wierz {
  int klucz;
  RB_Wierz *ojciec, *lewy, *prawy;
  int kolor;
};
const int CZERWONY=0;
const int CZARNY=1;

Naszym celem jest zaprogramować operację:

    RB_WstawWierz(RB_wierz *&korzen, int klucz);

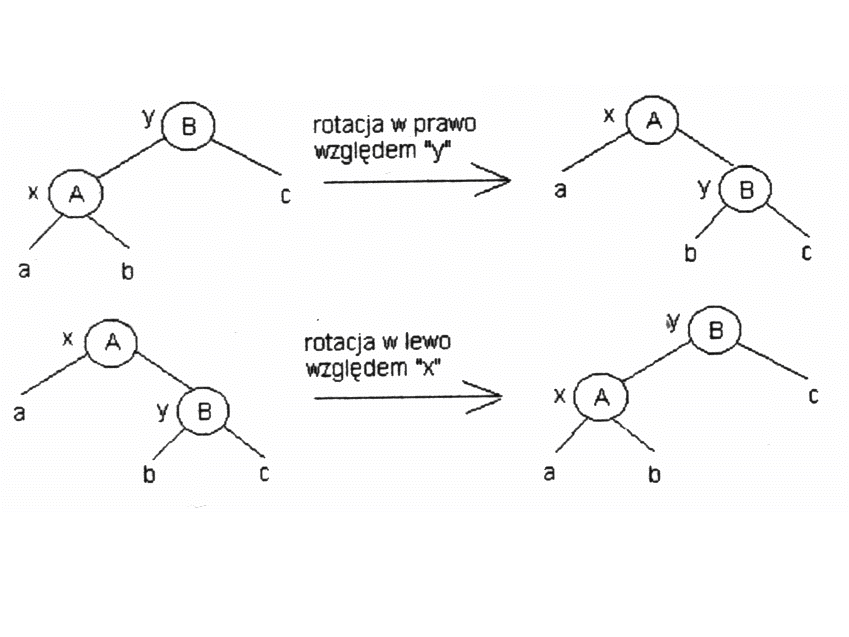
Zaczniemy od zaprogramowania pomocniczych operacji:

    RB_RotacjaWLewo(RB_wierz *x);
    RB_RotacjaWPrawo(RB_wierz *x);

których działanie zilustrowano na rysunku:

Zadanie 16

Zaimplementuj procedury:

    BST_RotacjaWLewo(BST_wierz *x);
    BST_RotacjaWPrawo(BST_wierz *x);

i sprawdz je na zwykłym drzewie BST z lekcji 6. Użyj procedury BST_PokazDrzewo() aby przekonać się że wszystko jest OK. Potem zamień "BST" na "RB".

Operacja wstawiania wierzchołków.

Procedura RB_WstawWierz() składa się z następujących trzech części:

Wstawiamy wierzchołek "x" jak w drzewach BST
oraz przyporządkowujemy mu kolor CZERWONY
.
Po wstawieniu wierzchołka może zostać zniszczona własność 3 (jeśli jego ojciec jest czerwony).
Konieczna jest pętla "naprawiająca" drzewo - zmieniająca kolory i wykonująca rotacje.
W pętli tej rozpatruje się 3 przypadki: w 1 przypadku zmienna "x" przemieszcza się w kierunku korzenia, w 2 i 3 przypadku pętla się kończy (przypadki są dokładnie wyjaśnione na rysunkach).
Pętla "kręci się" jeśli "x" nie jest korzeniem i jeśli kolor jego ojca jest czerwony.
W pętli rozpatrujemy 2 możliwości: gdy ojciec "x"-a jest lewym synem dziadka lub gdy jest prawym synem dziadka. Omówimy tylko sytuacje gdy jest lewym synem dziadka (w drugim przypadku postępuje się podobnie - należy tylko zamienić miejscami strony lewą i prawą).
Wszystkie 3 przypadki (razy 2 możliwości) które należy rozpatrywać w każdym obrocie pętli są przedstawione na poniższych rysunkach
.
Korzeniowi drzewa przyporządkowujemy kolor CZARNY (kolor korzenia mógł się zmienić podczas działania powyższej pętli !)
.

UWAGA 1:

Krawędzie na których jest problem z własnością 3 zaznaczam grubą linią.

Na poniższych rysunkach kolor szary oznacza CZARNY, natomiast kolor biały oznacza CZERWONY.

UWAGA 2:
Zauważ że operacje jakie wykonujemy na drzewie (patrz rysunki) zachowują własność 4.

Wprowadźmy oznaczenia:
        y   -stryj wierzchołka x (y=x->ojciec->ojciec->prawy)
        x1 -ojciec wierzchołka x
        x2 -dziadek wierzchołka x
(x, x1, x2, y - są wskazaniami na wierzchołki !)

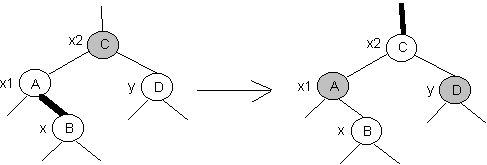
Przypadek 1:
zachodzi gdy "y->kolor == CZERWONY"
nie ma znaczenia czy "x" jest lewym czy prawym synem x1
zmieniamy kolory wierzchołków x1, y, x2
(przekłamanie nie zostaje usunięte !)
zmienna "x" przemieszcza się w kierunku korzenia: przypisanie x=x2

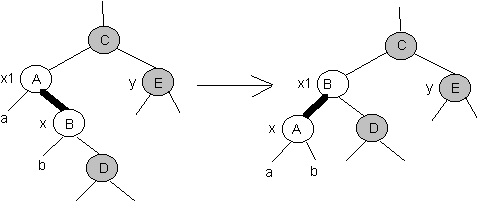
Przypadek 2:
zachodzi gdy "y->kolor == CZARNY" oraz gdy "x" jest prawym synem swojego ojca
wykonujemy rotacje w lewo względem x1
następnie przypisujemy x=x1
otrzymujemy sytuację dopuszczalną przez przypadek 3 i wykonujemy jego kod
(przekłamanie zostaje usunięte definitywnie - koniec pętli)

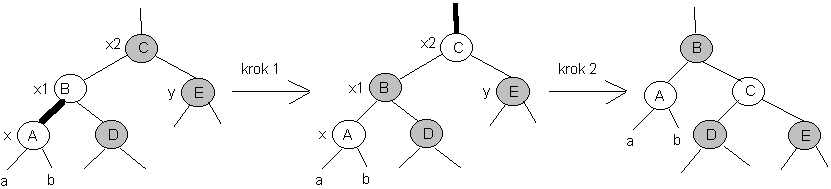
Przypadek 3:
zachodzi gdy "y->kolor == CZARNY" oraz gdy "x" jest lewym synem swojego ojca
zmieniamy kolory wierzchołków x1 i x2 (krok 1)
następnie dokonujemy rotacji w prawo względem x2 (krok2)
(przekłamanie zostaje usunięte definitywnie - koniec pętli)

Zadanie 17

Zaimplementuj procedury:

    RB_WstawWierz(RB_wierz *&korzen, int klucz);
    RB_PokazDrzewo(RB_wierz *korzen);

Sprawdz czy procedura RB_WstawWierz() działa prawidłowo, przy pomocy RB_PokazDrzewo(). Procedura RB_PokazDrzewo() powinna pokazywać wierzchołki drzewa w następujący sposób:

    klucz(klucz_ojca)[kolor], ...

Zadanie domowe 8

Zaimplementuj procedury:

    RB_UsunWierz(RB_wierz *&korzen, RB_wierz *x);

oraz

    RB_Wysokosc(RB_wierz *x, int &min, int &max);
    RB_WysokoscCzarna(RB_wierz *x, int &min, int &max);

oraz zmodyfikuj procedury dla drzew BST tak aby działaly dla drzew RB.

Sprawdz czy procedura RB_UsunWierz() działa, przy pomocy RB_PokazDrzewo().

Procedury RB_Wysokosc() i RB_WysokoscCzarna() zwracają długość najdłuższej i najkrótszej ścieżki od wierzchołka "x" do liści. W przypadku drugiej procedury chodzi tylko o ilość czarnych wierzchołków (wykluczając "x") w każdej takiej ścieżce. Jeśli uruchomimy te procedury dla korzenia oraz jeśli wszystko działa poprawnie to w przypadku RB_Wysokosc() powinno być: "max<=2*min", natomiast w przypadku RB_WysokoscCzarna() powinno być "max==min".

Zadanie domowe 9

Zbadaj średni czas działania procedury sortowania kubełkowego z lekcji 7, podobnie jak badaliśmy głębokość drzew BST na losowej permutacji. Przypominam że średni czas działania tej procedury jest liniowy względem "n" (patrz też zadanie 15 z lekcji 7).