Lekcja 8
drzewa, obchody drzew

Listy c.d.

Zadanie 120
Zaimplementuj następujące operacje na listach jednokierunkowych:

  1. Konkatenacja(L1, L2, var L3)
    czyli połączenie list L1 i L2 oraz umieszczenie wyniku w L3; wynik ma zawierać kopię elementów, nowy element listy tworzymy procedurą x<-nowyElement
  2. OdwrócKolejność(var L)
    odwracamy kolejność elementów listy; w tym wypadku nie tworzy się kopii elementów
  3. Długość(L)
    oblicza długość listy; koniecznie użyj rekurencji!
  4. Szukaj(L, wartość)
    szuka na liście elementu o podanej wartości i zwraca wskazanie na ten element, jeśli takiego elementu nie ma to zwraca nil; koniecznie użyj rekurencji!

 

Drzewa binarne.

Drzewo binarne składa się z elementów (obiektów) z których każdy posiada atrybuty: wartość, lewy, prawy, przy czym lewy i prawy wskazują na lewego i prawego "potomka" ...

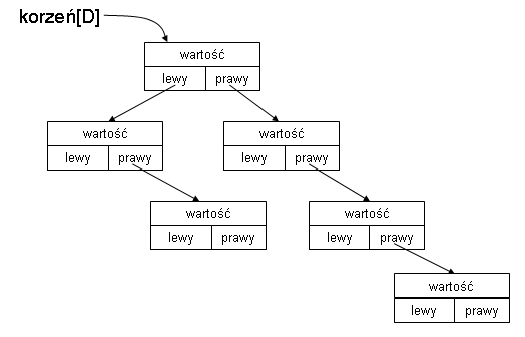
Drzewo reprezentujemy przez obiekt D z atrybutem korzeń. Wartości nil w atrybutach lewy i prawy są wykorzystywane w następujący sposób:

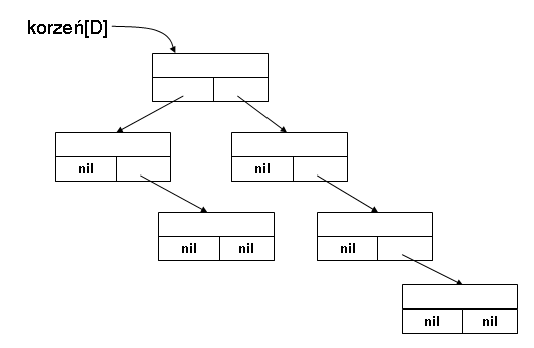
Zadanie 121
Zaimplementuj następujące operacje na drzewie binarnym:

  1. WypiszMetodąPreOrder(D)
    metoda PreOrder to rekurencyjna metoda wypisywania wartości elementów drzewa polegająca na tym że:
        a. wypisujemy wartość korzenia,
        b. wypisujemy wartości lewego poddrzewa,
        c. wypisujemy wartości prawego poddrzewa.
  2. WypiszMetodąInOrder(D)
    w tej metodzie wypisywania elementów zamieniamy miejscami (a) i (b)
  3. Zasymuluj działanie powyższych metod na poniższym drzewie:
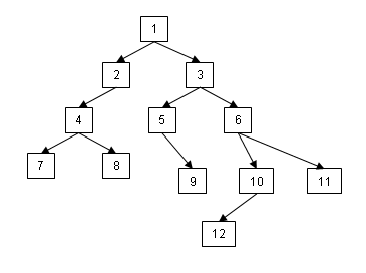
  4. WypiszMetodąWszerz(D)
    najpierw wypisujemy korzeń, potem elementu w odległości 1 od korzenia (1 poziom), potem 2 poziom itd.
    Wskazówka: można użyć pomocniczej tablicy której elementami są wskazania na elementy drzewa.
  5. Wysokość(D)
    procedura wypisuje wysokość drzewa, czyli największą odległość od korzenia do liścia ...
  6. wskazanie = Szukaj(D, wartość)
    szuka w drzewie elementu o podanej wartości i zwraca wskazanie na ten element, jeśli takiego elementu nie ma to zwraca nil
  7. zaimplementuj operację Szukaj(D, wartość) bez stosowania rekurencji!

Operacje słownikowe.

Przez operacje słownikowe rozumiemy następujące operacje:

Uwaga: prawdziwe zastosowania słownika wymagają aby element słownika zawierał parę (klucz, wartość); dla prostoty w poniższych zadaniach będziemy się posługiwać tylko wartością ...

Zadanie 122
Zaimplementuj operacje słownikowe:

  1. TAB_Wstaw(wartość)
  2. indeks = TAB_Szukaj(wartość)
    jeśli elementu nie ma to zwraca 0 (do przechowywania wartości używamy tablicy T[1..n])
  3. TAB_Usun(indeks)

przy pomocy tablicy, tak efektywnie jak to możliwe (chodzi o czas działania). Oszacuj czas działania tych 3 operacji przyjmując jako operację dominującą:
    a. porównywanie wartości
    b. przypisywanie wartości

 

Drzewa BST.

Drzewa BST to szczególny rodzaj drzew binarnych na których można efektywnie wykonywać operacje słownikowe ...

Kilka faktów:

  1. BST = Binary Search Tree
  2. Każdy wierzchołek x drzewa BST posiada atrybuty:
        wartość, lewy, prawy, rodzic
  3. Drzewo BST to drzewo binarne (niekoniecznie pełne) posiadające następującą własność:
        niech x wskazuje dowolny wierzchołek drzewa; 
        wszystkie wierzchołki lewego poddrzewa wierz x mają wartości < wartość[x] 
        wszystkie wierzchołki prawego poddrzewa wierz x mają wartości > wartość[x]

  Przykład drzewa BST:

 
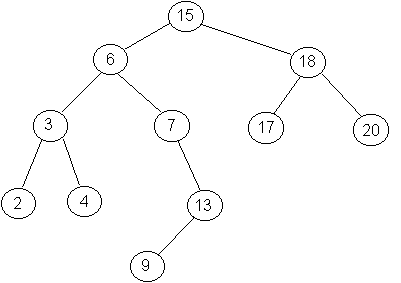
Założenie: dla uproszczenia zakładamy że wszystkie wartości w drzewie BST są różne !

Oto podstawowe operacje na drzewie BST:

BST_Wstaw(korzeń, nowy)
oczywiście nowy wierzchołek należy wstawiać tak aby nie popsuć własności drzewa BST; nowy wierzchołek wstawiamy zawsze jako liść drzewa, należy tylko wyszukać odpowiednie miejsce: sprawdzamy czy
    wartość[nowy] < wartość[korzen]
jeśli tak to wiemy że wierzchołek zostanie wstawiony w lewym poddrzewie, w przeciwnym wypadku zostanie wstawiony w prawym poddrzewie itd
 
wskazanie = BST_Maksimum(korzen)
wystarczy "iść" po prawej gałęzi drzewa BST, w kierunku od korzenia do liścia, tak długo jak to możliwe
 
wskazanie = BST_Następnik(wierzchołek)
1) jeśli wierzchołek posiada prawe poddrzewo, to wtedy zwracamy minimalny element w prawym poddrzewie
2) w przeciwnym wypadku szukamy wierzchołka takiego, że największym kluczem jego lewego poddrzewa jest wartość[wierzchołek]; innymi słowy idziemy od wierzchołka wskazywanego przez wierzchołek w górę drzewa tak długo aż napotkamy wierzchołek, który jest lewym synem swojego rodzica; wartość rodzica jest właśnie poszukiwanym następnikiem (na powyższym rysunku następnikiem 13 jest 15)
 
BST_Usuń(wierzchołek)
Uwaga: ta procedura jest dość skomplikowana !
należy rozważyć trzy przypadki:
1) wierzchołek jest liściem drzewa - wtedy zwyczajnie go usuwamy
2) wierzchołek ma tylko jednego potomka - wtedy dodajemy połączenie między rodzic[wierzchołek] i lewy[wierzchołek] (lub prawy[wierzchołek]), a sam wierzchołek usuwamy
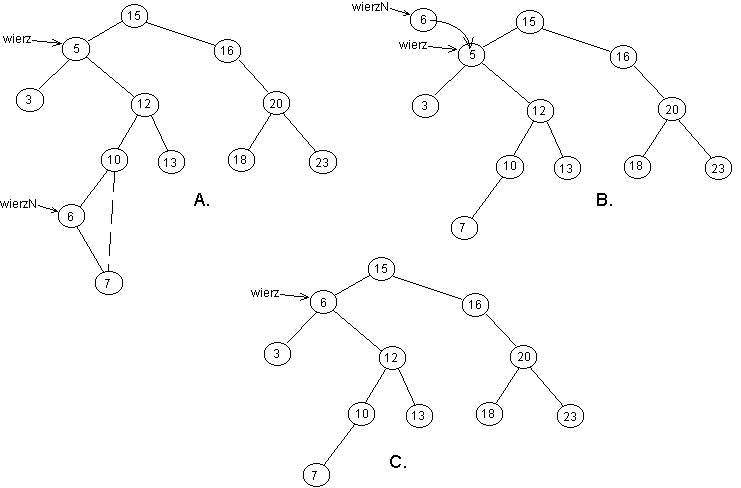
3) wierzchołek ma dwóch potomków - wtedy znajdujemy następnik wierzchołek; oznaczmy go przez wierzchołekN; o wierzchołekN wiemy że nie ma lewego potomka; dodajemy połączenie między rodzic[wierzchołekN] i prawy[wierzchołekN], następnie przepisujemy wartość wierzchołekN do wartości wierzchołek i usuwamy wierzchołekN.

Trzeci przypadek powyższej procedury jest przedstawiony na poniższym rysunku:

Zadanie 123
Zaimplementuj operacje słownikowe:

  1. BST_Wstaw(D, nowy)
    wstawia element wskazywany przez parametr nowy
  2. wskazanie = BST_Szukaj(D, wartość)
    szuka elementu o podanej wartości; jeśli elementu nie ma to zwraca nil
  3. BST_Usuń(D, wierzchołek)
    usuwa z drzewa element wskazywany przez wierzchołek (zachowując własność BST!)

przy pomocy drzewa BST. Oszacuj czas działania tych 3 operacji przyjmując jako operację dominującą porównywanie wartości.