Lekcja 9
kopce

Kopce.

Czym jest kopiec (ang. heap) ...

• kopiec jest "prawie pełnym" drzewem binarnym (tylko ostatni poziom nie musi być pełny)
• kopiec jest przechowywany w tablicy A[1..n] której elementami są liczby; tablica posiada dodatkowo atrybut heapSize[A]
• kopiec posiada tzw własność kopca:
          dla każdego wierzchołka o indeksie i (który nie jest korzeniem)
                     A[Parent(i)] >= A[i]
          gdzie Parent(i) jest indeksem rodzica wierzchołka o indeksie i

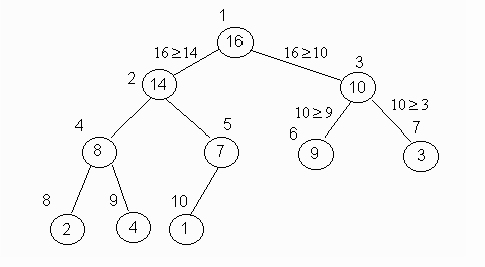
Przykład kopca:
Następującej tablicy:

A[1..15] = 16, 14, 10, 8,  7,  9,  3,  2,  4,  1,  ?,  ?,  ?,  ?,  ?
           1   2   3   4   5   6   7   8   9   10  11  12  13  14  15
heapSize[A]=10

odpowiada drzewo:

Zadanie 130
Zaimplementuj następującą procedurę służącą do "naprawiania" niekompletnego kopca ...

Procedura Heapify(A, i)

• W tej procedurze zakłada się, że obaj synowie wierzchołka i są kopcami, natomiast i niekoniecznie jest kopcem, co oznacza że może być A[i] < A[left(i)] lub A[i] < A[right(i)]. Celem tej procedury jest taka modyfikacja tablicy A aby i stało się kopcem.
  Uwaga: Mówiąc że "i jest kopcem" rozumiem, że poddrzewo binarne którego korzeniem jest i jest kopcem (czyli posiada własność kopca).
• Opis procedury:  Oznaczmy przez l i r lewego i prawego syna i.  Procedura znajduje największą z liczb A[i], A[l], A[r].  Jeśli jest to A[l] wtedy przestawia się miejscami elementy i-ty i l-ty, przez co psujemy kopiec l, dlatego konieczne jest rekurencyjne (?) wywołanie procedury dla l. W przypadku gdy największy jest A[r] postępujemy analogicznie. Oczywiście jeśli największe jest A[i] wtedy nic nie trzeba robić.
• Jeśli i jest indeksem pewnego wierzchołka drzewa to dostęp do ojca oraz do lewego i prawego potomka tego wierzchołka uzyskujemy przy pomocy funkcji: Parent(i), Left(i), Right(i) - które należy zdefiniować!

Następnie wypróbuj jej działanie na następującym kopcu:

A[1..15] = 7,  10, 6,  9,  3,  4,  5,  1,  8,  2,  ?,  ?,  ?,  ?,  ?,  ?
           1   2   3   4   5   6   7   8   9   10  11  12  13  14  15
heapSize[A]=10

zakładając że procedurę uruchomiono z parametrami (A, 1).
 

Zastosowanie kopca: sortowanie/ HeapSort.

Zadanie 131
Zaimplementuj procedurę HeapSort i pomocniczą procedurę BuildHeap opisane niżej:

Procedura BuildHeap(A)

• Procedura ta otrzymuje tablicę A[1..n] z dowolną zawartością (heapSize[A]=n) i zamienia ją w kopiec.
• Opis procedury:  Procedura ta przegląda wierzchołki drzewa od dolnej warstwy (przegląda tablicę od końca) i uruchamia Heapify() dla każdego wierzchołka. Gwarantuje to że jeśli uruchamiamy Heapify(A,i) to synowie i już są kopcami! Zauważmy, że liście drzewa są kopcami z natury rzeczy, dlatego procedura BuildHeap() może rozpoczynać działanie od wierzchołka który nie jest liściem. Biorąc pod uwagę że mamy tu "prawie" pełne drzewo binarne można łatwo wyznaczyć indeks pierwszego (od końca) wierzchołka, który nie jest liściem.
• "Na oko" czas działania tej procedury wynosi O(n log n), jednak dokładniejsza analiza biorąca pod uwagę że "dużo poddrzew ma małą wysokość" pokazuje że czas ten wynosi O(n).

Procedura HeapSort(A)

• Wiemy że korzeń drzewa (czyli element o indeksie 1) jest większy od wszystkich pozostałych elementów tablicy A.  Dlatego zamieniamy go miejscami z ostatnim elementem tablicy, a następnie zmniejszamy heapSize[A] o 1. Synowie korzenia są kopcami, ale sam korzeń może naruszyć własność kopca, dlatego konieczne jest wywołanie procedury Heapify(A,1).
• Czas działania procedury HeapSort to O(n log n).
   

Zastosowanie kopca: kolejka priorytetowa.

Kolejka priorytetowa to zbiór elementów posiadających atrybuty "key" (klucz) oraz "value" (wartość), na którym można wykonywać następujące operacje:

Procedure HeapInsert(S,x)

Wstawia do kolejki element x (x jest obiektem z atrybutami key[x] i value[x])

Function HeapMaximum(S)

Odczytuje wartość elementu o największym kluczu.

Function HeapExtractMax(S)

Odczytuje i usuwa z kolejki element o największym kluczu.
 

Zadanie 132
Zaimplementuj kolejkę priorytetową przy pomocy kopca. Oszacuj czas działania wszystkich operacji.

Dodatkowe założenia: Elementy kolejki powinny być przechowywane w tablicy S[1..n]; elementy tej tablicy są obiektami z atrybutami key i value; zakładamy że dysponujemy operacją Heapify() używająca wartości key[] każdego elementu tablicy.

Wskazówka do operacji HeapInsert(S,x): dodajemy nowy element x jako liść drzewa (na koniec kopca); oczywiście ojciec x może nie spełniać własności kopca. Istnieje ścieżka od x do korzenia drzewa. Przesuwamy x po tej ścieżce, w kierunku korzenia, aż nie znajdziemy dla niego właściwego miejsca (przesuwanie polega na "zamianie miejscami" z ojcem). Zauważmy, że mimo przesuwania x, drzewo o korzeniu w x jest zawsze kopcem - nie jest to takie całkiem oczywiste ...
 

Zadanie 133
Do kolejki priorytetowej dodaj operacje:

Procedure HeapChangeKey(S,i,newKey )

Operacja ta zmienia klucz elementu o indeksie i zachowując własność kopca.