Lekcja 10
algorytmy stabilne numerycznie

Algorytmy stabilne numerycznie.

Numeryczna stabilność.
Algorytm jest niestabilny numerycznie jeśli w trakcie obliczeń "akumuluje się" błąd numeryczny i w rezultacie powstaje mało dokładny wynik

Cecha i mantysa.
Liczbę rzeczywistą można przedstawić w postaci:

m * 10^c

gdzie "m" to mantysa (m należy do przedziału [0.1,1)), a "c" to cecha (c jest liczba całkowitą).

Zmiennopozycyjna arytmetyka t -cyfrowa.
Liczby rzeczywiste są reprezentowane w komputerze w postaci:

(mantysa, cecha)

przy czym mantysa jest zapisywana przy użyciu t -cyfr.

Uwaga 1: Dla uproszczenia będziemy używać dziesiętnego systemu zapisu liczb.
Uwaga 2: Mantysę zapisujemy w pamięci komputera bez początkowego zera (oszczędzamy w ten sposób pamięć).

Przykład 1: Zapis 5 -cyfrowy liczby 123.456789012345 to 0.12346*10^3; czyli 123.46
(w ostatnią cyfrę mantysy trzeba zaokrąglić!!! 0-4:+0, 5-9:+1)

Obliczenia w arytmetyce t -cyfrowej.
Aby obliczyć wartość "wyrażenia arytmetycznego prostego" (składającego się z jednej dwuargumentowej operacji arytmetycznej) postępujemy tak:

1. Dane są argumenty operacji arytmetycznej (m1,c1), (m2,c2), gdzie m1 i m2 są zapisane na t -cyfrach.
2. Wykonuje się (dokładnie) operację arytmetyczną na argumentach.
3. Wynik operacji zapisuje się w postaci (m3,c3), gdzie m3 jest zapisane na t -cyfrach; może się okazać że część cyfr dokładnego wyniku zostanie bezpowrotnie stracona; pamiętać o prawidłowym zaokrągleniu ostatniej cyfry mantysy!!!

Aby obliczyć wartość "wyrażenia arytmetycznego złożonego" rozkładamy je na elementarne operacje arytmetyczne i postępujemy jak opisano wyżej.

Przykład 2:  Obliczanie wartości wyrażenia 0.12341234 - 0.123 w arytmetyce 4 -cyfrowej.
Przedstawiamy argumenty w postaci (m,c) w arytmetyce 4 -cyfrowej:
    0.12341234 = 0.1234*10^1 = 0.1234,
    0.123           = 0.123*10^1   = 0.123, 
wykonujemy operacje arytmetyczna:
    0.1234 - 0.123 = 0.0004
i przedstawiamy wynik w postaci (m,c):
    0.4*10^(-3) = 0.0004
podczas gdy dokładny wynik to 0.00041234 = 0.4123*10^(-3).

Wniosek z przykładu 2:
Odejmowanie bliskich sobie liczb wprowadza duży błąd numeryczny ...

..................................................................................

Zadanie 140
(Przykład pokazujący że odejmowanie bliskich liczb wprowadza duży błąd numeryczny!)
Rozwiąż równanie

x^2 + p*x + q = 0 dla p= -6.433, q= 0.009474

używając arytmetyki 4 -cyfrowej, na trzy sposoby:

1. Korzystając ze wzorów x1= (-p - sqrt(p^2 - 4q))/2, x2= (-p + sqrt(p^2 - 4q))/2.
2. Korzystając ze wzorów x2= (-p + sqrt(p^2 - 4q))/2, x1*x2=q.
3. Korzystając z kalkulatora (i jego k -cyfrowej arytmetyki, gdzie k jest stosunkowo duże).

Następnie porównaj wyniki ...

..................................................................................

Zadanie 141
(Rozwiązywanie równania f(x)=0 metodą stycznych [Newtona])
Podaj algorytm rozwiązujący równanie f(x) = 0 metodą stycznych sugerowaną przez poniższy rysunek. Zakładamy że dane są funkcje f(x) oraz ff(x) obliczająca pochodną funkcji f. Algorytm ma się kończyć gdy kolejne przybliżenie różni się o mniej niż eps od poprzedniego przybliżenia. Na poniższym rysunku literami x0, x1, x3, ... oznaczono kolejne przybliżenia rozwiązania równania.

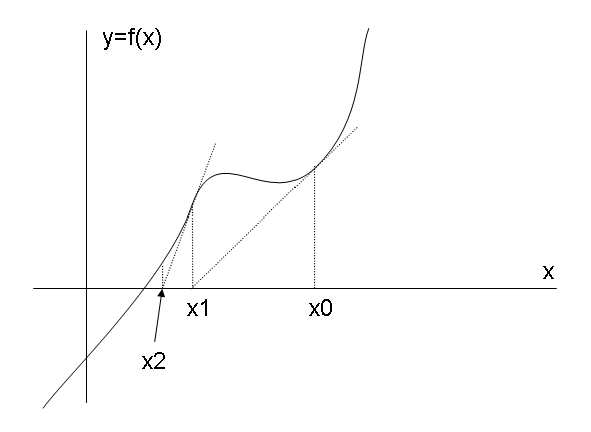
Zadanie 141.1
Podaj algorytm obliczający sqrt(x).

Zadanie 142
(Rozwiązywanie równania f(x)=0 metodą siecznych [?]).
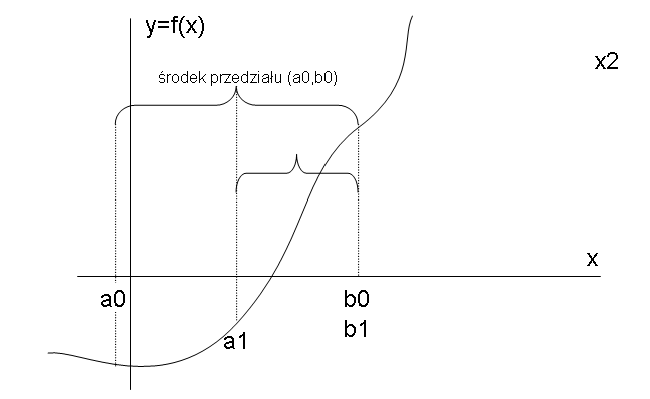
Podaj algorytm rozwiązujący równanie f(x) = 0 metodą sugerowaną przez poniższy rysunek. Na poniższym rysunku widać przedziały (a0,b0), (a1, b1), ... które na pewno zawierają rozwiązanie równania. Obliczenia mają się zakończyć gdy rozmiar przedziału jest < eps.

Zadanie 143
(Aproksymacja całki oznaczonej przy pomocy trapezów)
Podaj algorytm obliczający (przybliżoną) wartość całki oznaczonej z funkcji f, w przedziale [a,b]. W obliczeniach należy wykorzystać trapezy o szerokości eps.

Zadanie 144
(Aproksymacja całki oznaczonej przy pomocy wielomianów 3 stopnia)
Podaj algorytm obliczający (przybliżoną) wartość całki oznaczonej z funkcji f, w przedziale [a,b]. W obliczeniach należy wykorzystać pseudo-trapezy o szerokości eps, których górna krawędź NIE jest odcinkiem tylko krzywą wielomianu 3 stopnia. Wielomian ten powinien się zgadzać na końcach przedziału co do wartości oraz co do wartości pochodnych. (Dlaczego używamy wielomianów akurat stopnia 3 ?)