Szkic algorytmu Kruskala:

1. W grafie G jest "las spinajacy", który początkowo składa się z pojedynczych wierzchołków.
2. Sortujemy krawędzie grafu G, niemalejąco, wg wag.
3. Następnie dla każdej krawędzi {v,u}, w kolejności niemalejących wag:
• Sprawdzamy czy {v,u} łączy dwa różne drzewa lasu. Jeśli tak to dodajemy tę krawędź do naszego lasu (przez co liczba drzew w lesie zmniejsza się o jeden).
4. Po przejściu przez wszystkie krawędzie otrzymujemy pojedyncze drzewo (można udowodnić, że jest to właśnie mininalne drzewo spinające ...)

Każde drzewo lasu jest reprezentowane przez zbiór wierzchołków (zbiory te są rozłączne).

1. Musimy mieć możliwość tworzenia zbiorów jednoelementowych (reprezentujących początkowy las).
2. Mając dwa wierzchołki "v" i "u" musimy mieć możliwość sprawdzenia czy należą one do różnych zbiorów.
3. Musimy mieć możliwość łączenia dwóch zbiorów wierzchołków

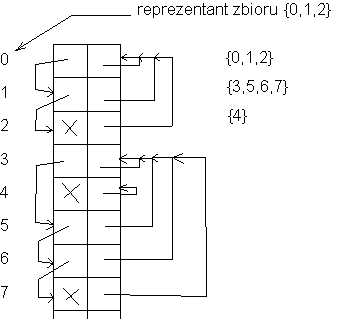
Należy zaimplementować następujące funkcje:

/* --------------------------------------------
   implementacja rozlacznych zbiorow
   --------------------------------------------
*/
struct ElZbioru {
  ElZbioru *nastepny;
  ElZbioru *reprezentant;
};

ElZbioru Zbior[N];

void UtworzZbior(int a) // a=0..N-1
{
  // tworzy 1-elementowy zbior z reprezentantem "a"
}

int ZnajdzZbior(int a)
{
  // zwraca reprezentanta zbioru zawierajacego "a";
  // jeśli dla elementow "b" i "c" ta funkcja
  // zwroci tego samego reprezentanta, to oznacza to że
  // oba elementy należą do tego samego zbioru !
}

void SumaZbiorow(int a, int b)
{
  // laczy zbior zawierajacy "a" ze zbiorem zawierajacym "b"
  // reprezentantem sumy zbiorow moze byc dowolny jej element
}

void PokazZbiory() // tylko do celow testowych ...
{
}

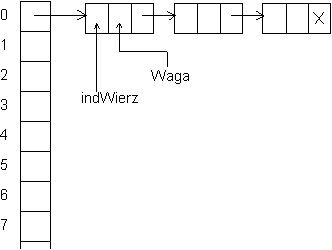
Należy zaimplementować następujące funkcje:

/* --------------------------------------------
   implementacja grafu (listy sasiadow)
   --------------------------------------------
*/
struct Sasiad {
  Sasiad *nastepny;
  int IndWierz;
  int Waga;
};

Sasiad *Graf[N];

void DodajKrawedz(int v, int u, int Waga)
{
  // nalezy kontrolowac czy nie ma "krawedzi wielokrotnych"
}

void PokazGraf() // tylko do celow testowych ...
{
}

/* --------------------------------------------
   sortowanie krawedzi wg wag
   --------------------------------------------
*/
struct KrawZWaga {
  int v,u,Waga;
};

KrawZWaga Krawedz[N*N];
int IloscKraw=0;

void KrawedzieDoTablicy()
{
  // przepisuje krawedzie z grafu do tablicy "Krawedz"
  // aktualizując odpowiednio zmienna "IloscKraw"
}

void SortujKrawedzie() // niemalejaco wg wag
{
}

void WypiszKrawedzie() // tylko do celow testowych ...
{
}

/* --------------------------------------------
   Algorytm MST Kruskala
   --------------------------------------------
*/
struct KrawZWaga2 {
  int v,u,Waga;
  KrawZWaga2 *nastepny;
};

KrawZWaga2 *ListaA;

void DodajKrawDoListyA(int v, int u, int Waga)
{
}

void PokazListeAorazLacznaWage()
{
}

void Kruskal()
{
  // algorytm ...
}

main()
{
  printf("\n\n----------------------------------------\n");

  /*
  // prosty przyklad ...
  //
  DodajKrawedz(0,1,1000);
  DodajKrawedz(1,2,999);
  DodajKrawedz(2,0,1000);
  PokazGraf();

  KrawedzieDoTablicy();
  SortujKrawedzie();

  Kruskal();

  PokazListeAorazLacznaWage();
  */

  DodajKrawedz(0,1,8);
  DodajKrawedz(1,2,7);
  DodajKrawedz(3,0,4);
  DodajKrawedz(4,1,2);
  DodajKrawedz(1,8,4);
  DodajKrawedz(2,5,9);
  DodajKrawedz(3,6,8);
  DodajKrawedz(6,4,7);
  DodajKrawedz(7,4,6);
  DodajKrawedz(6,7,1);
  DodajKrawedz(7,8,2);
  DodajKrawedz(2,8,14);
  DodajKrawedz(8,5,10);
  PokazGraf();

  KrawedzieDoTablicy();
  SortujKrawedzie();

  Kruskal();

  PokazListeAorazLacznaWage();
  // Waga drzewa powinna być = 37 !!!
}

Zadanie domowe 3

Zadanie domowe 4

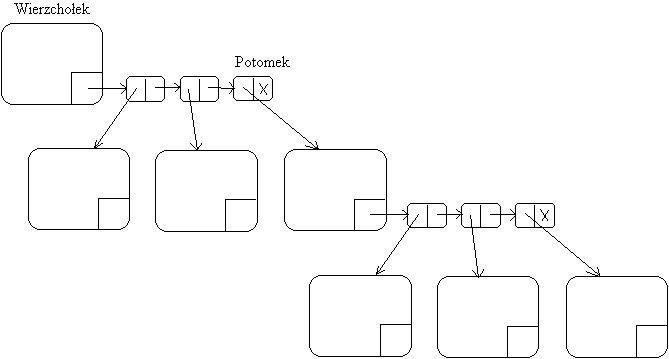
   1.uzyskiwanie wskazania na strukturę Wierzchołek na podstawie identyfikatora wierzchołka
   2.dodawanie potomka do dowolnego wierzchołka drzewa
   3.wypisywanie elementów drzewa (dowolnym sposobem)