... przypominam że należy napisać sprawozdanie z wykonania każdego zadania i pod koniec zajęć przesłać je na odpowiedni adres email-owy

sprawozdanie powinno zawierać:

Zadanie 9

Ciąg Fibonacciego definiujemy następująco: 
    f[1]=1, f[2]=1, f[n]=f[n-1]+f[n-2] dla n>2
zaprogramuj dwie funkcje obliczające wartość n-tego elementu ciągu Fibonacciego: 
    function Fib_R(n:integer):integer;
    function Fib_I(n:integer):integer;
z których pierwsza oblicza wartość "rekurencyjnie" (czyli wywołuje samą siebie z mniejszym parametrem), a druga jest "iteracyjna" czyli NIE używa rekurencji.
Pokaż ile jest wykonywanych operacji "+" w obu funkcjach dla n=6 i wiekszych, w formie odpowiedniej tabelki drukowanej przez program (być może warto rozważyć użycie zmiennych typu "longint" zamiast "integer").
 

Zadanie 10

Napisz funkcję obliczającą wartość symbolu Newtona "n po k", oznaczaną tutaj przez N(n,k), dla 0<=n<=50, 0<=k<=n, przy pomocy odpowiedniej macierzy pomocniczej. Obliczanie wartości ma się sprowadzać do odczytania stosownego elementu tej macierzy.
Do zbudowania macierzy pomocniczej użyj następującej własności: 
    N(n,k) = N(n-1,k-1) + N(n-1,k)
Będzie to tzw "trójkąt Pascala". Uwaga: nie wolno wypełniać macierzy pomocniczej wartościami N(n,k) obliczonymi bezpośrednio z definicji symbolu Newtona (z malymi wyjatkami).
Zademonstruj działanie funkcji na kilku przykładach.
 

Zadanie 11

Dana jest "macierz" A[1..n,1..m]. Posortuj jej elementy przy pomocy procedury znajdującej element minimalny. Sortowanie ma wyglądać następująco: 
    A[1,1]<=A[1,2]<= ... <=A[1,m]<=
    A[2,1]<= ...         <=A[2,m]<=
    .............................
    A[n,1]<= ...         <=A[n,m]
Wygeneruj losową macierz i ją wydrukuj (wiersz po wierszu). Następnie posortuj i znów ją wydrukuj. Uwaga: niedopuszczalne jest rozwiazanie polegajace na "przepisaniu elem. macierzy do tablicy, posortowaniu, i przepisaniu spowrotem".

Zadanie 11a
Wyznacz liczbę różnych elementów w macierzy posortowanej w zadaniu 11.
 

Zadanie 12 (*)

Dana jest "kostka" V[1..n,1..m,1..p]. Posortuj jej elementy przy pomocy procedury znajdującej element minimalny. Sortowanie ma wyglądać następująco: 
    V[1,1,1]<= ...         <=V[1,m,1]<=
    V[2,1,1]<= ...         <=V[2,m,1]<=
    .................................
    V[n,1,1]<= ...         <=V[n,m,1]<=

    V[1,1,2]<= ...         <=V[1,m,2]<=
    V[2,1,2]<= ...         <=V[2,m,2]<=
    .................................
    V[n,1,2]<= ...         <=V[n,m,2]<=

    .................................

    V[1,1,p]<= ...         <=V[1,m,p]<=
    V[2,1,p]<= ...         <=V[2,m,p]<=
    .................................
    V[n,1,p]<= ...         <=V[n,m,p]
Wygeneruj losową kostkę i ją wydrukuj (warstwa po warstwie). Następnie posortuj i znów ją wydrukuj.

Zadanie 12a (*)
Wyznacz liczbę różnych elementów w kostce posortowanej w zadaniu 12.
 

Zadanie 13

Lista jednokierunkowa wygląda następująco:

Zaimplementuj następujące operacje na liście jednokierunkowej: 
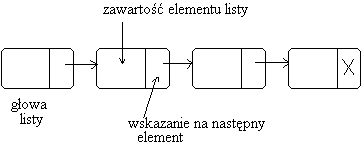
    struct ElementListy {...};
      // struktura reprezentujące pojedynczy element listy

    struct Lista {...};
      // struktura reprezentujące listę

    void NowaLista(Lista &l);
      // inicjowanie struktury Lista

    void DodajElementOdGłowy(Lista &l, ElementListy &elem);

    void DodajElementOdOgona(Lista &l, ElementListy &elem);

    void PokazListe(Lista &l);
      // pokazuje elementy listy począwszy od "głowy"

    void PolaczListy(Lista &l1, Lista &l2);
      // lista "l2" zostaje dołączona na koniec listy "l1" 
      // ("l2" staje się pustą listą)
Wszystkie operacje (także DodajElementOdOgona !) mają działać "w stałym czasie", tj w czasie który nie zależy od liczby elementów list. Elementy list należy tworzyć dynamicznie (język C: operatory new/delete lub funkcje malloc/free, język Pascal: funkcje new/dispose).