... przypominam
że należy napisać sprawozdanie z wykonania każdego zadania i pod koniec
zajęć przesłać je na odpowiedni adres email-owy
sprawozdanie powinno zawierać:
-
nazwisko, imię, nr indeksu osoby wykonującej sprawozdanie
-
kod programów
-
wyniki eksperymentów (wkleić do sprawozdania przy
pomocy "schowka MS Windows")
(są też zadania domowe !!!)
Zadanie 14
Zdefiniuj następujące funkcje (używając rekurencji):
-
n^k; Potega(n,k); korzystając z własności n = n * n^(k-1)
-
n!; Silnia(n); korzystając z własności n! = n * (n-1)!, 0!=1
-
Newton(n,k); korzystając z własności Newton(n,k) = Newton(n-1,k-1)
+ Newton(n-1,k)
Należy wypróbować działanie tych funkcji dla małych
liczb.
UWAGA 1 : pamiętaj o używaniu "dużych" zmiennych
całkowitych.
UWAGA 2 : pamiętaj że rekurencja nie może być
"nieskończona" !!!
Zadanie 15
Zaimplementuj procedury wypisujące wszystkie "obiekty kombinatoryczne"
danego typu (np K-elementowe kombinacje zbioru N-elementowego). Przy
użyciu rekurencji jest to bardzo proste zadanie !
Kazda procedura ma wypisywać wszystkie obiekty (ponumerowane) a na końcu
- dla kontroli - powinna wypisywać prawidłową liczbę obiektów (tu będą
przydatne funkcje zdefiniowane w zadaniu 14; np liczba wspomnianych kombinacji
to Newton(N,K)).
Należy zaimplementować procedury wypisujące następujące obiekty:
-
K-elementowe wariacje Z powtórzeniami zbioru N-elementowego {1,
..., N}
są to wszystkie ciągi K-elementowe zbioru N-elementowego
ich liczba wynosi = N^K
-
K-elementowe wariacje BEZ powtórzeń zbioru N-elementowego
ich liczba wynosi = N!/(N-K)!
-
K-elementowe kombinacje zbioru N-elementowego
są to wszystkie podzbiory K-elementowe zbioru N-elementowego
[przypominam że {1,2} i {2,1} to ten sam zbiór !]
ich liczba wynosi = Newton(N,K)
-
K-elementowe kombinacje Z powtórzeniami zbioru N-elementowego
ich liczba wynosi = Newton(N+K-1,K)
Należy używać podanych niżej stałych, zmiennych, typów i procedur:
const N=7; K=4;
type t_tablica=array[1..K] of integer;
var Wynik:t_tablica; Licznik:longint;
(* tej procedury nalezy uzywac
do wypisywania "obiektu kombinatorycznego"
*)
procedure PokazWynik;
var j:integer;
begin
Licznik:=Licznik+1;
write(Licznik:4,':');
for j:=1 to K do write(Wynik[j]:2,',');
writeln;
end;
{ prototypy procedur }
procedure WariacjeZPowtorzeniami(i:integer);
procedure WariacjeBezPowtorzen(i:integer);
procedure Kombinacje(i:integer);
procedure KombinacjeZPowtorzeniami(i:integer);
function Potega(n,k:longint):longint;
function Silnia(n:longint):longint;
function Newton(n,k:longint):longint;
(* w ten sposob nalezy testowac procedury *)
begin
{Licznik:=0;
WariacjeZPowtorzeniami(1);
writeln('WariacjeZPowtorzeniami: Potega(',N,',',K,')=',Potega(N,K));
}
Licznik:=0;
WariacjeBezPowtorzen(1);
writeln('WariacjeBezPowtorzen: powinno byc=',Silnia(N)/Silnia(N-K):6:2);
end.
Wskazówka:
jak zaprogramować WariacjeZPowtorzeniami(i) ???
... użyjemy tablicy "Wynik" do przechowywania pojedynczej wariacji;
w procedurze WariacjeZPowtorzeniami
w pętli "for j:=1 to N do" robimy następujące rzeczy:
Wynik[1]:=j
uruchamiamy całą procedure rekurencyjnie ale w taki sposób aby modyfikowała
tablicę Wynik od drugiego elementu (taka jest właśnie interpretacja parametru
"i" procedury WariacjeZPowtórzeniami - jego wartość to indeks elementu
tablicy Wynik ktory procedura powinna bezpośrednio modyfikować )
UWAGA: nie wolno używać parametrów i zmiennych lokalnych o nazwach
"n" i "k" gdyż są już stałe o tych nazwach.
Zadanie 16
Dana jest "kostka" V[1..n,1..m,1..p]. Posortuj jej elementy przy pomocy
procedury znajdującej element maksymalny. Sortowanie ma wyglądać
następująco:
V[1,1,1]<= ... <=V[1,m,1]<=
V[2,1,1]<= ... <=V[2,m,1]<=
.................................
V[n,1,1]<= ... <=V[n,m,1]<=
V[1,1,2]<= ... <=V[1,m,2]<=
V[2,1,2]<= ... <=V[2,m,2]<=
.................................
V[n,1,2]<= ... <=V[n,m,2]<=
.................................
V[1,1,p]<= ... <=V[1,m,p]<=
V[2,1,p]<= ... <=V[2,m,p]<=
.................................
V[n,1,p]<= ... <=V[n,m,p]
Wygeneruj losową kostkę i ją wydrukuj (warstwa po warstwie). Następnie
posortuj i znów ją wydrukuj.
Zadania domowe.
Zadanie domowe 1
Lista jednokierunkowa wygląda następująco:
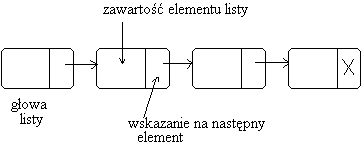
Zaimplementuj następujące operacje na liście jednokierunkowej:
struct ElementListy {...};
// struktura reprezentujące pojedynczy element listy
struct Lista {...};
// struktura reprezentujące listę
void NowaLista(Lista &l);
// inicjowanie struktury Lista
void DodajElementOdGłowy(Lista &l, ElementListy &elem);
void UsunElementOdGłowy(Lista &l);
void DodajElementOdOgona(Lista &l, ElementListy &elem);
void PokazListe(Lista &l);
// pokazuje elementy listy począwszy od "głowy"
void PolaczListy(Lista &l1, Lista &l2);
// lista "l2" zostaje dołączona na koniec listy "l1"
// ("l2" staje się pustą listą)
Wszystkie operacje (także DodajElementOdOgona !) mają działać "w
stałym czasie", tj w czasie który nie zależy od liczby elementów list.
Elementy list należy tworzyć dynamicznie (język C: operatory new/delete
lub funkcje malloc/free, język Pascal: funkcje new/dispose).
Zadanie domowe 2
Wiadomo że "naiwne" algorytmy sortujące działają w czasie O(n^2) a
te bardziej wyrafinowane (jak QuickSort i MergeSort) w czasie O(n log n)
...
Zaplanuj eksperyment pokazujący że istotnie tak jest.
Przez czas działania rozumiemy: A) liczbę porównań elementów ciągu, B)
liczbę przypisać elementu tablicy.
Należy używać losowych ciągów danych.
Należy użyć jednego algorytmu naiwnego (przez wstawianie, przez selekcje)
i jednego nie-naiwnego.
Należy zmieniać odpowiednio wartość "n" (=liczby elementów) i dla każdego
"n" obliczać czas działania obu algorytmów na ciągu tych samych n-liczb.
Następnie czas działania algorytmów należy zestawić z wartościami funkcji
(n^2) i (n log n) w formie tabelki:
n | 10 | 20 | .......
n^2 | ? | ? |
n log n | ? | ? |
algorytm naiwny | ?,? | ?,? |
algorytm nie-naiwny | ?,? | ?,? |
Należy kilkakrotnie powtórzyć obliczenia dla ustalonego "n" i wynik uśrednić,
gdyż czas działania może zależeć od rodzaju danych wejściowych.
