1 : |4,3,2,1, |  , , , , |  , , , , |
   2 : |4,3,2, , | 1, , , , |  , , , , |
   3 : |4,3, , , | 1, , , , | 2, , , , |
   4 : |4,3, , , |  , , , , | 2,1, , , |
   5 : |4, , , , | 3, , , , | 2,1, , , |
   6 : |4,1, , , | 3, , , , | 2, , , , |
   7 : |4,1, , , | 3,2, , , |  , , , , |
   8 : |4, , , , | 3,2,1, , |  , , , , |
   9 : | , , , , | 3,2,1, , | 4, , , , |
  10 : | , , , , | 3,2, , , | 4,1, , , |
  11 : |2, , , , | 3, , , , | 4,1, , , |
  12 : |2,1, , , | 3, , , , | 4, , , , |
  13 : |2,1, , , |  , , , , | 4,3, , , |
  14 : |2, , , , | 1, , , , | 4,3, , , |
  15 : | , , , , | 1, , , , | 4,3,2, , |
  16 : | , , , , |  , , , , | 4,3,2,1, |

Zadanie 18 (?)

Zadanie 19 (*)

(Poniżej przedstawiam przy pomocy rysunków niezbędne pojęcia ...)
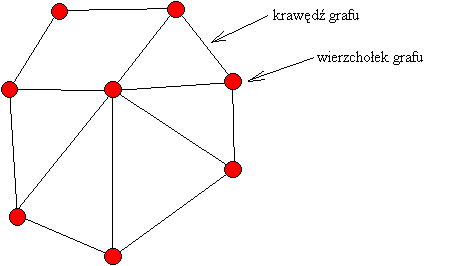
Co to jest graf ?
Ten rysunek pokazuje przykładowy graf:

Co to jest drzewo ?
Jest to graf który nie zawiera cykli; poniższy rysunek pokazuje przykładowe drzewo:

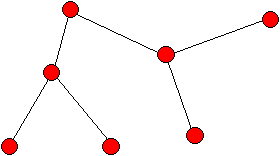
Zauważmy że pojedynczy wierzchołek też jest drzewem.
Zbiór rozłącznych drzew nazywamy lasem.

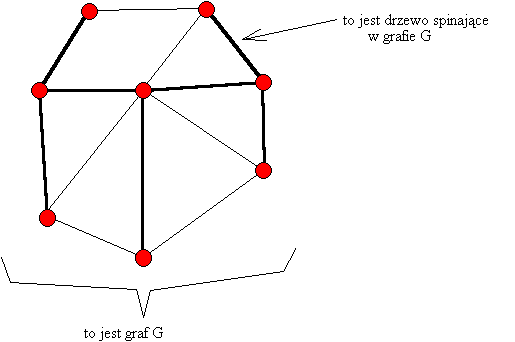
Co to jest drzewo spinające ?
Jest to drzewo zawarte w grafie, zawierające wszystkie jego wierzchołki; poniższy rysunek pokazuje przykładowe drzewo spinające:
 
 
 

Dany jest graf G, którego krawędziom przyporządkowano "wagi".  Minimalne drzewo spinające (=MST) to drzewo zawierające wszystkie wierzchołki grafu, takie że suma wag jego krawędzi jest minimalna (w porównaniu z sumą wag krawędzi innych drzew spinających).  Minimalne drzewo spinające można znaleźć przy pomocy algorytmu Kruskala ...

 

Szkic algorytmu Kruskala:

1. Na początku w grafie G jest "las spinajacy" który składa się z pojedynczych wierzchołków (wszystkich wierzchołków grafu G).
2. Sortujemy krawędzie grafu G, niemalejąco, wg wag.
3. Następnie przebiegamy po posortowanych krawędziach i dla krawędzi {v,u}wykonujemy:
• Sprawdzamy czy {v,u} łączy dwa różne drzewa lasu. Jeśli tak to "dodajemy" tę krawędź do naszego lasu (przez co liczba drzew w lesie zmniejsza się o jeden - gdyż z dwóch drzew zrobi się jedno).
• Zapamiętujemy dodaną krawędź w specjalnej "tablicy wynikowej".
4. Po przejściu przez wszystkie krawędzie otrzymujemy pojedyncze drzewo (można udowodnić, że jest to właśnie mininalne drzewo spinające ...). Krawędzie tego drzewa znajduja się w tablicy wynikowej.

Każde drzewo lasu jest reprezentowane przez zbiór wierzchołków (zbiory te są rozłączne).

1. Musimy mieć możliwość tworzenia zbiorów jednoelementowych (reprezentujących początkowy las).
2. Mając dwa wierzchołki "v" i "u" musimy mieć możliwość sprawdzenia czy należą one do różnych zbiorów.
3. Musimy mieć możliwość łączenia dwóch zbiorów wierzchołków

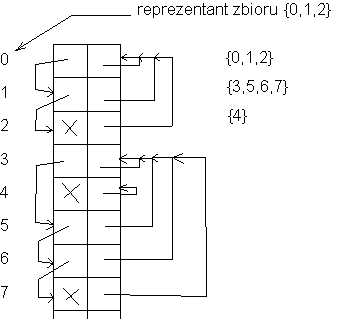
void UtworzZbior(int a)
{
  // tworzy 1-elementowy zbior z reprezentantem "a"
}

int ZnajdzZbior(int a)
{
  // zwraca reprezentanta zbioru zawierajacego "a";
  // jeśli dla elementow "b" i "c" ta funkcja
  // zwroci tego samego reprezentanta, to oznacza to że
  // oba elementy należą do tego samego zbioru !
}

void SumaZbiorow(int a, int b)
{
  // laczy zbior zawierajacy "a" ze zbiorem zawierajacym "b"
  // reprezentantem sumy zbiorow moze byc dowolny jej element
}

void PokazZbiory() // tylko do celow testowych ...
{
}

void DodajKrawedz(int v, int u, float Waga)
{
  // dodaje krawędź między wierzchołkami "v" i "u"
  // z wagą równą "Waga"
  // (wagi można przechowywać w osobnej macierzy ...)
}

void PokazGraf() // tylko do celow testowych 
{
}

main()
{
  printf("\n\n----------------------------------------\n");

  /*
  // prosty przyklad ...
  //
  DodajKrawedz(0,1,1000);
  DodajKrawedz(1,2,999);
  DodajKrawedz(2,0,1000);
  PokazGraf();

  KrawedzieDoTablicy();
  SortujKrawedzie();

  Kruskal();

  PokazDrzewoOrazJegoWage();
  */

  DodajKrawedz(0,1,8);
  DodajKrawedz(1,2,7);
  DodajKrawedz(3,0,4);
  DodajKrawedz(4,1,2);
  DodajKrawedz(1,8,4);
  DodajKrawedz(2,5,9);
  DodajKrawedz(3,6,8);
  DodajKrawedz(6,4,7);
  DodajKrawedz(7,4,6);
  DodajKrawedz(6,7,1);
  DodajKrawedz(7,8,2);
  DodajKrawedz(2,8,14);
  DodajKrawedz(8,5,10);
  PokazGraf();

  KrawedzieDoTablicy();
  SortujKrawedzie();

  Kruskal();

  PokazDrzewoOrazJegoWage();
}