Zadanie A "przy tablicy"

Zadanie 25

    struct ElementListy { 
      ElementListy *nastepny, *poprzedni;
      int liczba; // "zawartość" elementu listy
    }; 
      // struktura reprezentujące element listy;
      // kazdy element listy zawiera "liczbę"

    struct Lista {
      ElementListy *glowa, *ogon;
    };
      // struktura reprezentujące listę

    void NowaLista(Lista &l);
      // tworzy pustą listę

    void DodajElement(Lista &l, int liczba, int gdzie);
      // gdzie = GŁOWA lub OGON
      // (!!!)

    void UsunElement(Lista &l, int gdzie);
      // usuwanie elementu z jednego z końców listy
      // (!!!)

    int ListaJestPusta(Lista &l);
      // zwraca 1 jeśli lista jest pusta, w przeciwnym wypadku zwraca 0

    void PokazListe(Lista &l, int gdzie);
      // parametr "gdzie" decyduje od którego końca pokazujemy listę

    void UsunCalaListe(Lista &l);

Kopce; algorytm HeapSort

To drzewo binarne jest "prawie" pełne - ostatni poziom drzewa nie musi być pełny.

Tablica A powinna posiadać atrybuty:

length[A] = długość tablicy
heapSize[A] = liczba początkowych elementów tablicy, które należą do kopca
                       (jest możliwe że heapSize[A] < length[A])

    int Parent(int i) { /* należy je samodzielnie zaprogramować ! */ }
    int Left(int i)   { /* ... */ }
    int Right(int i)  { /* ... */ }

A[i] = 16, 14, 10, 8,  7,  9,  3,  2,  4,  1
  i    1   2   3   4   5   6   7   8   9   10

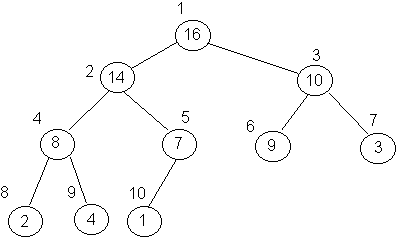
Poniżej opisuję pewne procedury wykonujące operacje na kopcu ...

Uwaga: Mówiąc że "i jest kopcem" rozumiem, że drzewo binarne którego korzeniem jest "i-ty element tablicy A" jest kopcem (czyli posiada własność kopca).

Procedura Heapify(A,i)

Zakłada się, że synowie wierzchołka "i" są kopcami, natomiast sam "i" niekoniecznie, to jest wartość A[i] może być mniejsza od wartości swoich synów.  Celem tej procedury jest taka modyfikacja tablicy A, aby "i" stało się kopcem.

Opis procedury:  Oznaczmy przez "l" i "r" lewego i prawego syna "i".  Procedura znajduje największą z liczb A[i], A[l], A[r].  Jeśli jest to A[l] wtedy przestawia się elementy i-ty i l-ty, przez co psujemy kopiec "l", dlatego konieczne jest rekurencyjne wywołanie procedury dla "l".  W przypadku gdy największy jest A[r] postępujemy podobnie.  Oczywiście jeśli największe jest A[i] wtedy nic nie trzeba robić.

Czas działnia tej procedury jest równy wysokości drzewa, czyli O(log n), gdzie n=heapSize[A].

Procedura ta orzymuje tablicę A z dowolnymi liczbami (heapSize[A] = length[A]) i zamienia ją w kopiec (dokładniej, drzewo o korzeniu 1 ma być kopcem).

Opis procedury:  Procedura ta przegląda wierzchołki drzewa od dolnej warstwy (przegląda tablicę od końca) i uruchamia Heapify(...) dla każdego elementu.  Gwarantuje to że jeśli uruchamiamy Heapify(A,i)  to synowie "i" już są kopcami !.  Zauważmy, że liście drzewa są kopcami z natury rzeczy, dlatego procedura BuildHeap() rozpoczyna działanie od wierzchołka który nie jest liściem. Biorąc pod uwagę że mamy tu "prawie" pełne drzewo binarne można łatwo wyznaczyć indeks pierwszego (od końca) wierzchołka, który nie jest liściem.

"Na oko" czas działnia tej procedury wynosi O(n log n), jednak dokładniejsza analiza biorąca pod uwagę że poddrzewa mają coraz mniejszą wysokość pokazuje że czas ten wynosi O(n).
 

Wiemy że korzeń drzewa (czyli element o indeksie 1) jest większy od wszystkich pozostałych elementów tablicy A.  Dlatego zamieniamy go z ostatnim elementem tablicy, a następnie zmniejszamy heapSize[A] o 1.  Synowie korzenia są kopcami, ale sam korzeń może naruszyć własność kopca, dlatego konieczne jest wywołanie procedury Heapify(A,1).

Czas działania procedury HeapSort to O(n log n)
 

    struct Heap {
      int length; // długość tablicy
      int heapSize;
      int *A; // indeksujemy od 1 !!!
    };

void Heapify(Heap& H, int i);
int BuildHeap(Heap& H);
void HeapSort(Heap& H);

Kolejki priorytetowe (przy pomocy kopców)

Procedura Insert(S,x)

Wstawianie do kolejki elementu "x" (z kluczem "key[x]")

Odczytywanie wartości elementu o największym kluczu.

Usuwa z kolejki element o największym kluczu.

    struct Elem {
      int key; // klucz elementu
      int value; // wartość elementu
    };    
    struct HeapPri {
      int length;
      int heapSize;
      Elem *A; // indeksujemy od 1 !!!
    };

int HeapPri_Maximum(HeapPri& H);

void HeapPri_ExtractMax(HeapPri& H);

void HeapPri_Insert(HeapPri& H, int key, int value);

Zadanie 28

void HeapPri_ChangeKey(HeapPri& H, int i, int key);