AAL260 - ćw - temat A

1. Zaliczenie z ćwiczeń

W czasie trwania zajęć piszemy sprawozdanie z wykonania Zadań danego tematu ...
W sprawozdaniu powinny się znaleźć:
Sprawozdanie to wysyłamy na adres mhanckow@main.amu.edu.pl subject: AAL260 - tematX
Termin nadsyłania sprawozdań: 2 tygodnie od ćwiczeń na których dany temat był omawiany.

2. Przydatne narzędzia programistyczne

Mały kompilator języka C pod Windows o nazwie "tcc":
  1. link do pliku tcc-0.9.23.zip; rozpakować go w dowolnym katalogu, jest tam skrypt cc.bat pokazujacy jak włączać kompilator (trzeba zmienić ściezki do katalogów w tym pliku !!!)
  2. dokumentacja C/C++
Wizualizacja grafów:

3. Zadania

Uwaga: we wszystkich zadaniach należy:
  - zaprogramować algorytm i wyprobuj jego działanie dla różnych danych
  - kod programu i wydruki działania wstawić do sprawozdania

................................................................

Zadanie 1 "rotacja cykliczna"
WE: tablica liczb int A[1..n], c -liczba całkowita z przedziału [-n, n]
WY: rotacja cykliczna tablicy A o c -elementów (jeśli c<0 to przesuwamy "w lewo").
Uzasadnij dlaczego algorytm działa poprawnie (słownie w sprawozdaniu).
Zaprogramuj algorytm i wyprobuj jego działanie na ciągu liczb, dla różnych wartości n i c.
Kod programu i wydruki działania wstaw do sprawozdania.
Wymagania:
  1. pesymistyczna złożoność czasowa ma wynosić O(n), czyli czas NIE zależy od c
  2. złożoność pamięciowa ma być O(1), czyli NIE można używać pomocniczej tablicy długości c ani n
Wskazówka: rozważ osobno przypadki gdy n dzieli się przez c i gdy się nie dzieli ...

Zadanie 2 "scalanie wierszy macierzy"
WE: M[1..n, 1..m] - macierz prostokątna liczb int; wiersze macierzy są posortowane "<=" (niemalejąco).
WY: posortuj "<=" elementy macierzy M i umieść wynik w tablicy W[1..n*m];
Wymagania:
  1. możliwie mała złożoność pesymistyczna czasowa; należy oszacować tę złożoność i słownie uzasadnić;
      (... mogę zdradzić że zlożoność ta powinna wynosić O(n m logn), jesli n jest liczbą wierszy macierzy)
  2. złozoność pamięciowa O(n*m)
Wskazówka: scalaj wiersze macierzy tak jak to się robi w MergeSort; przepisanie macierzy do tablicy W
oraz posortowanie (algorytmem O(n^2)) nie jest optymalnym rozwiązaniem ...

Zadanie 2.5 "szybkie a^n"
Podaj procedurę podnoszącą "a" do potęgi "n" w czasie znacząco mniejszym od n;
trywialnie można to zrobić przy pomocy (n-1) operacji mnożenia;
operacja dominująca: działanie arytmetyczne (głównie mnożenie).

................................................................

Zadanie 3 "implementacja operacji na drzewie BST"
Zaimplementuj wszystkie poznane operacje na drzewie BST
(tj BST_Insert, BST_Search, BST_Minimum, BST_Następnik, BST_Usuń)
Opis drzew BST oraz operacji na nich znajdziesz:
  1. na slajdach z wykładu nr 1
  2. tutaj: asd22008.htm - Zadanie 20 (bez operacji usuwania wierzchołka)
      opis operacji usuwania jest tutaj: asd22009.htm - Zadanie 22
W sprawozdaniu umieść kod Twojej implementacji
oraz test jej działania następującej postaci:
  ciag operacji na drzewie BST
  obraz powstałego drzewa BST (gif lub tekstowy obraz drzewa BST)
  .... od nowa

Zadanie 4 "oczekiwana wysokość drzewa BST"
Zbadaj oczekiwaną wysokość drzewa BST powstałego przez wstawianie elementów z losowej permutcji liczb {1, ..., n}. Wskazówki jak to zrobić znajdziesz tutaj: asd22009.htm - Zadanie 21.

Zadanie 4.1 "wysokość BST bez rekurencji"
Wprowadź do drzewa BST możliwość obliczania wysokości dowolnego wierzchołka drzewa w STAŁYM czasie.  Czas działania innych operacji powinien pozostać (asymptotycznie) taki sam!

Zadanie 4.2 "ulepszanie drzew BST"
Ulepsz drzewo BST tak aby operacje wykonywały się "znacząco" szybciej niż na zwykłym drzewie BST (zwykłe BST: jeśli drzewo zawiera n -elementów to operacje wykonują się w czasie pesymistycznym O(n)).  Ulepszone BST powinno posiadać te same operacje co zwykłe BST.  Wolno używać "losowości".  Dodatkowo, eksperymentalnie potwierdź skuteczność swojego rozwiązania (oznacza to, że trzeba - oczywiście - zaimplementować zaproponowane rozwiązanie...).
Uwaga: "znacząco" oznacza że nie chodzi o poprawienie stałego czynnika w oszacowaniu czasu działania...
Uwaga 2: najlepszym ulepszeniem drzew BST są oczywiście drzewa RB, ale w tym zadaniu chodzi o znacznie prostsze i nie tak doskonałe rozwiązanie ...

Zadanie 5 "implementacja operacji RB_Insert"
Zaimplementuj operacje RB_Insert na drzewie RB.
Materiały o drzewach RB: asd220_rb.htm oraz slajdy wykładu 1.
Operacje rotacji oraz wstawiania elementu prosze wykonać całkowicie "po swojemu" tj nie wzorując się na procedurze z książki Cormena.
Wyprobuj działanie RB_Insert dla pewnych ciągów danych, zwłaszcza takich na których drzewa BST zachowują się źle (jakie to ciągi?).
Wykonaj także wizualizację powstałego drzewa RB.

Zadanie 6 "różne implementacje słownika"
Porównaj fizyczny czas wykonywania operacji słownikowych (Insert, Serach, Delete) na tym samym ciągu danych, gdy słownik jest zaimplementowany na następujące sposoby:
    1. przy pomocy drzewa BST
    2. przy pomocy drzewa RB
    3. przy pomocy haszowania (patrz: asd22013.htm rozdział "Tablice z haszowaniem")
Klucze elementów słownika powinny być napisami (porównywanymi przy pomocy strcmp()).
Dane do eksperymentu (klucze) wyciągnij z pliku const.txt w Zadaniu 32 z asd22013.htm.
Zbadaj czas wstawiania elementów do słownika (wszystkich elem z pliku const.txt).
Zbadaj czas znajdowania elementów w słowniku (maksymalny i średni po wszystkich elem z const.txt).
(Nie możemy badać czasu usuwania, gdyż nie mamy impl. RB_Delete).
Czas fizyczny w języku C odczytamy funkcją clock()/ time.h;
w j. Tcl można użyć komendy time {kod}.


................................................................


Zadanie 7 "szybkie modulo"
WE: a, b - liczby całkowite, >=0
WY: r= a mod b (czyli reszta z dzielenie a przez b)
Wymaganie dodatkowe:
1. wolno używać wyłącznie działań arytmetycznych +,-,*
2. liczba działań arytmetycznych wykonywanych przez algorytm powinna być znacząco mniejsza niż a/b (gdybyśmy obliczali "a mod b" przy pomocy odejmowania to właśnie tyle działań byśmy wykonali ...)

Zadanie 8 "przekrój zbiorów w plikach"
Zakladamy, że każdy zbiór jest trzymany w osobnym pliku (tekstowym), a element zbioru to linia tekstu.
Mamy k zbiorów w plikach zbior1.txt, zbior2.txt ... zbior_k.txt.
Cel: obliczyć przekrój tych zbiorów w możliwie krótkim czasie a wynik umieścić w pliku zbior_wynikowy.txt.
Można pomocniczo używać poleceń systemowych do wykonania tego zadania;
można także używać pomocniczo plików tymczasowych.
Rozwiązanie zadania składa się z progrmu i ew. skryptu oraz wydruku eksperymentu pokazującego,
że przedstawione rozwiązanie istotnie działa.
Dodatkowo należy oszacować czas działania jako funkcję n = n1+n2+...+n_k,
gdzie n_i to rozmiar zbioru plik_i.txt.

Zadanie 9 "szukanie liczb"
Napisz algorytm znajdujący liczby naturalne
    1<= i, j, k, l <= 20
takie że i^3 + j^3 + k^3 = l^3.
Wymaganie dodatkowe: postaraj się NIE sprawdzać wszystkich możliwych 20^3 wartości zmiennych i, j, k.

Zadanie 10 "obiekty kombinatoryczne"
Zaimplementuj procedury wypisujące wszystkie "obiekty kombinatoryczne" danego typu:
Wskazówka: Jak zaprogramować WariacjeZPowtorzeniami(i) ?
Używamy tablicy Wynik[1..n] do przechowywania pojedynczej wariacji.
W procedurze WariacjeZPowtorzeniami(i), w pętli "for j<- 1 to N do" wykonujemy:
        1) Wynik[i]<- j
        2) uruchamiamy rekurencyjnie WariacjeZPowtorzeniami(i+1)
Zasada działania procedury jest następująca:
zakres tablicy Wynik[1..i-1] zawiera fragment wariacji utworzony przez poprzednie wywołania procedury;
procedura WariacjeZPowtorzeniami(i) bezpośrednio modyfikuje element Wynik[i];
rekurencyjne wywołanie WariacjeZPowtorzeniami(i+1) generuje wszystkie możliwe wariacje w zakresie Wynik[i+1..n];
oczywiście gdy wszystkie elementy tablicy Wynik mają przypisaną wartość to należy ją wypisać.

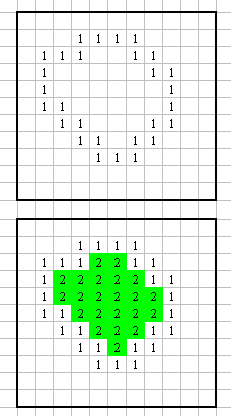
Zadanie 11 "wypełnianie konturu"
 Dana jest macierz M[1..n, 1..n] reprezentująca obraz.
W macierzy tej za pomocą 1 jest reprezentowany kontur, pozostałe elementy zawierają 0.
Napisz algorytm wypełniający kontur wartością 2.
W rozwiązaniu oprócz kodu programu należy wstawić wydruki pokazujące obraz przed i po wypełnieniu.