Algorytm Prima znajdujący MST.

Opis algorytmu Prima:

w algorytmie tym mamy do czynienia zawsze z pojedynczym drzewem do którego dodajemy po jednek krawędzi;

na poczatku drzewo składa sie z jednego wierzchołka (dowolnego)

sposród wszystkich krawędzi które mają dokładnie jedna końcówke w bieżącym drzewie wybieramy krawędź z najmniejszą wagą i dodajemy ją do bieżącego drzewa

proces ten kontynuujemy tak długo aż nie otrzymamy drzewa spinającego

.....................

Jest oczywiste, że drzewo jakie otrzymamy jest spinające.
Można udowodnić że jest ono minimalnym drzewem spinającym (czyli MST)
[patrz: Cormen, str 565, Tw 24.1].

graf wejściowy ma być reprezentowany przy pomocy listy sąsiedztw (czyli tak jak na tym rysunku)

jedyny problem stanowi wybieranie najlżejszej krawędzi, co należy robić efektywnie;
robimy to przy pomocy kolejki priorytetowej:
--> każdemu wierzchołkowi "v" nie należącemu do bieżącego drzewa odpowiada element kolejki priorytetowej (który w tym momencie także oznaczamy przez "v");
--> element "v" kolejki ma następujące pola:

v.sasiad  // nr sąsiada wierzchołka "v"
v.waga  // waga krawędzi {v,v.sąsiad}
pole "waga" pełni rolę klucza w kolejce priorytetowej (będziemy "wyciągać" z kolejki element z najmniejszą wagą);
--> wierzchołek "v" może być połączony z bieżącym drzewem przy pomocy kilku krawędzi; krawędź {v,v.sąsiad} to najlżejsza z tych krawędzi; "v.waga" to waga tej krawędzi;
można to zobaczyć na poniższym rysunku:


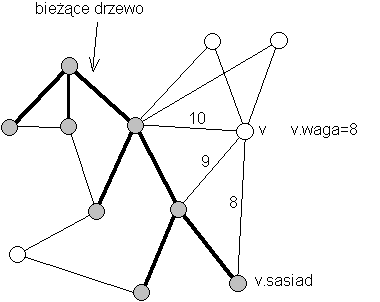
jeśli wierzchołek "v" nie jest połączony z bieżącym drzewem wtedy v.waga=nieskończoność

Uwaga 1: po dodaniu nowej krawędzi do bieżącego drzewa trzeba zaktualizować kolejkę priorytetową !
jeśli dodaliśmy do drzewa kraw "u,v" (przy czym "v" jest nowym wierzchołkiem w drzewie) to należy zaktualizować w kolejce priorytetowej wszystkich sąsiadów wierzchołka "v" (nie należących do drzewa);
można to zobaczyć na poniższym rysunku:


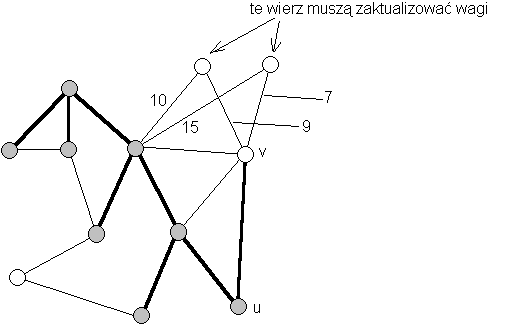
Uwaga 2: należy nadać odpowiednie wartości początkowe polom "waga" i "sasiad" w kolejce priorytetowej; należy być także ostrożnym jeśli chodzi o pierwszy krok procedury ...
 

// DodajKrawedz(wierz1, wierz2, waga);
DodajKrawedz(0, 1, 8.0);
DodajKrawedz(1, 2, 7.0);
DodajKrawedz(3, 0, 4.0);
DodajKrawedz(4, 1, 2.0);
DodajKrawedz(1, 8, 4.0);
DodajKrawedz(2, 5, 9.0);
DodajKrawedz(3, 6, 8.0);
DodajKrawedz(6, 4, 7.0);
DodajKrawedz(7, 4, 6.0);
DodajKrawedz(6, 7, 1.0);
DodajKrawedz(7, 8, 2.0);
DodajKrawedz(2, 8, 14.0);
DodajKrawedz(8, 5, 10.0);
// Waga drzewa MST powinna być = 37 !!!

Zadanie 30

Wskazówki do kolejki priorytetowej z drzewa BST:
.......................................

Wskazówki do kopcowej kolejki priorytetowej:
Każdy wierzchołek grafu jest powiązany z elementem kolejki priorytetowej i odwrotnie. Pamiętajmy jednak że elementy kolejki się przesuwają !!!.

Kolejka priorytetowa wymaga dodatkowej procedury:

     void HeapPri_ChangeKey(A,i,klucz);

     void HeapPri_ExtractMax(A, &Elem);

Zadanie 31(*)